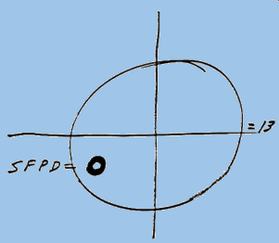
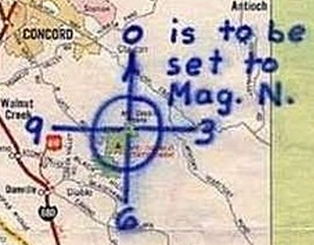
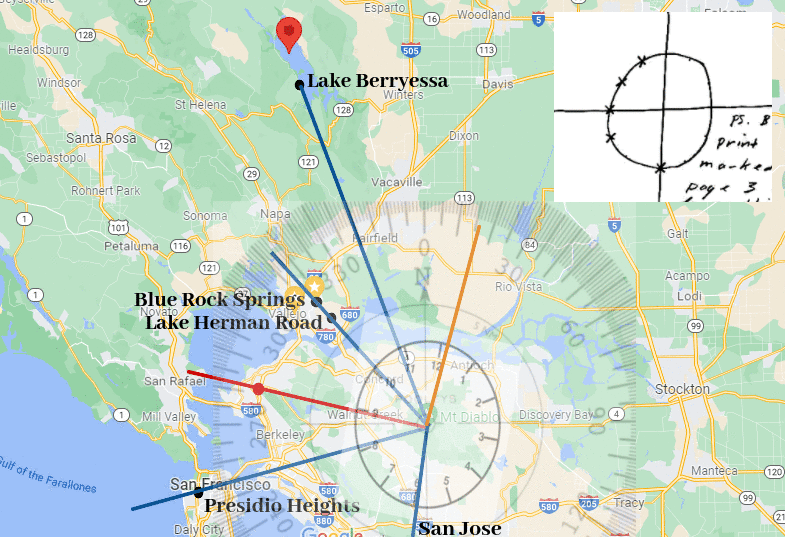
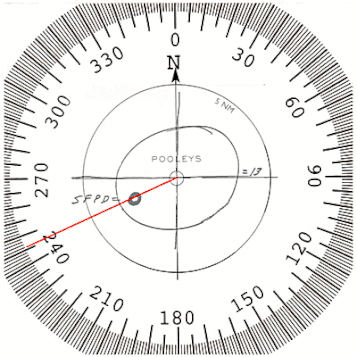
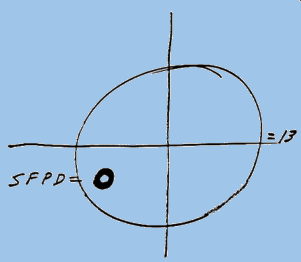
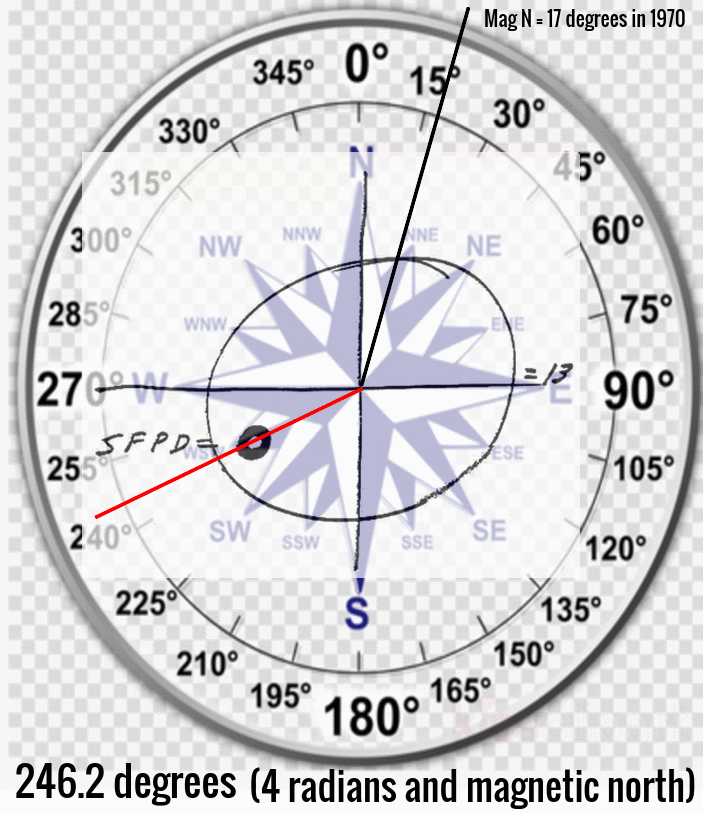
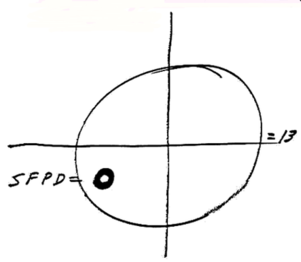
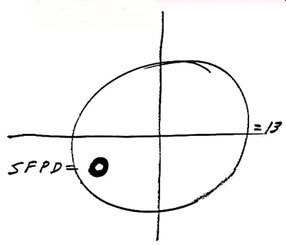
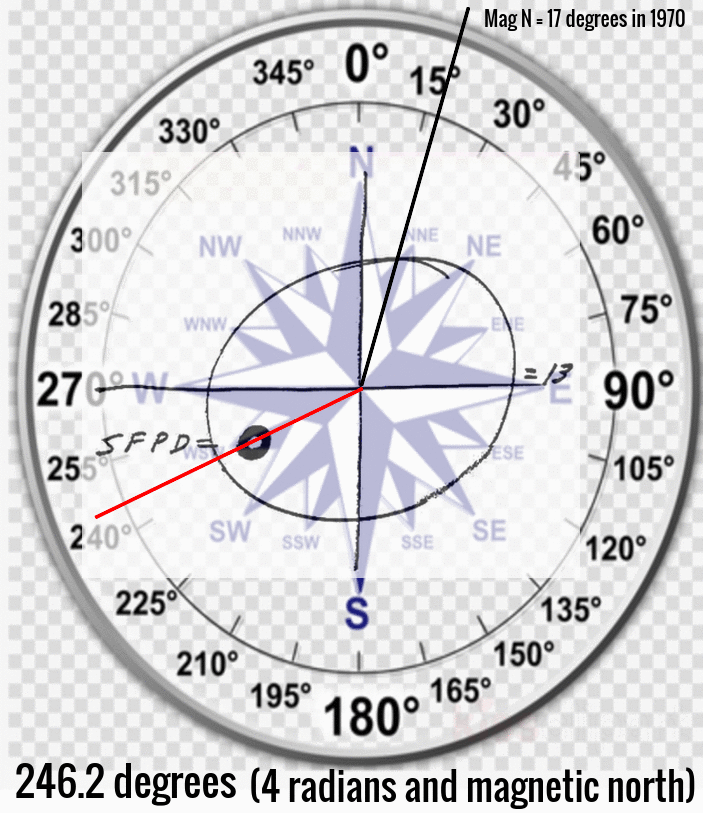
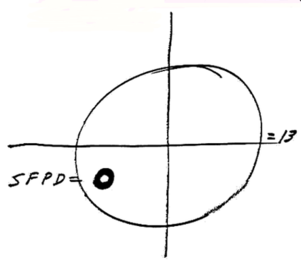
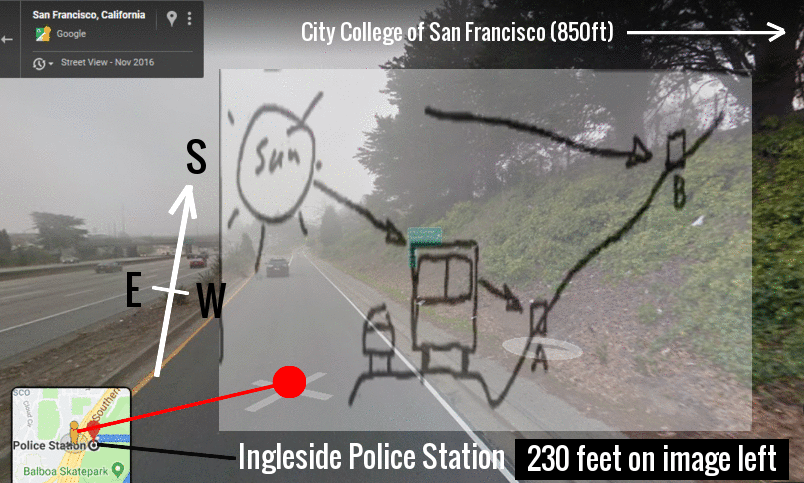
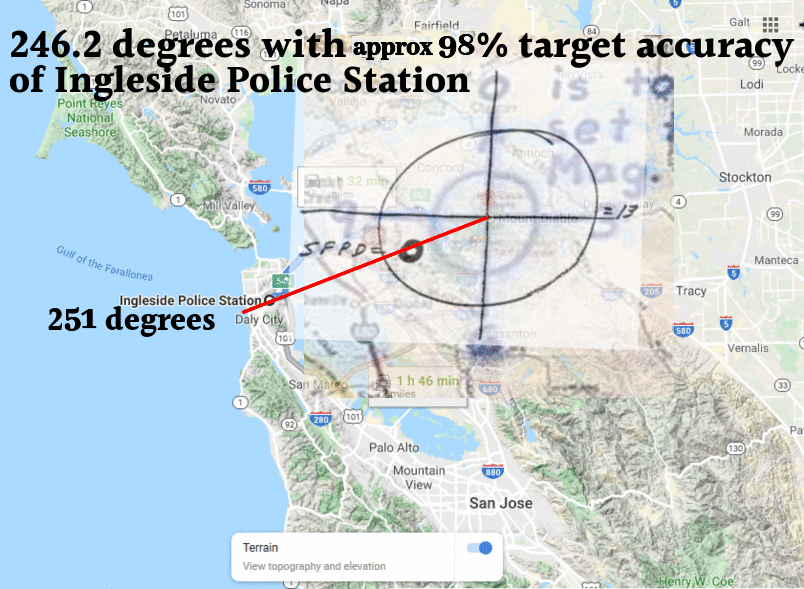
The center of the red circle is 246.2 degrees, showing the inaccuracy of the crude drawing by Zodiac
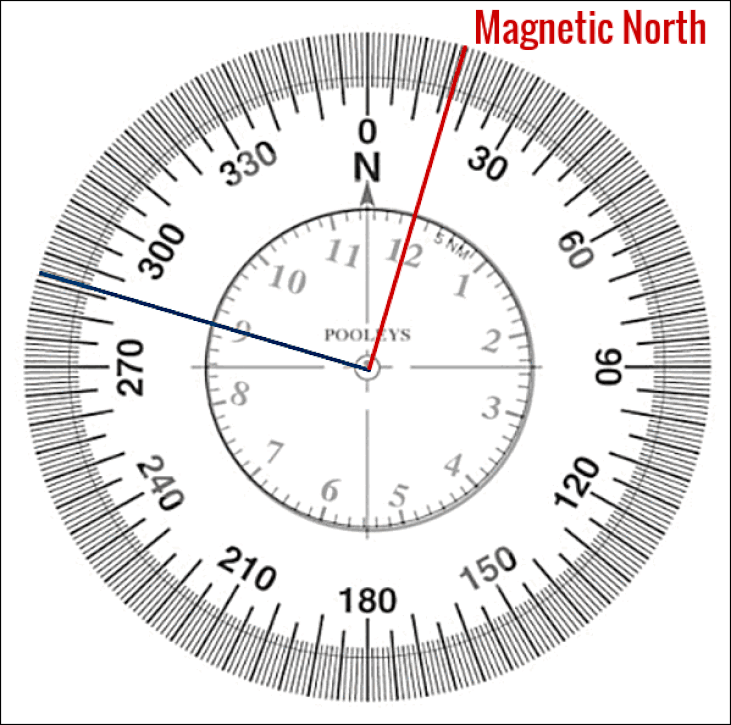
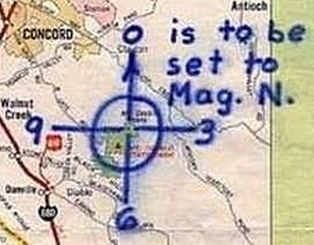
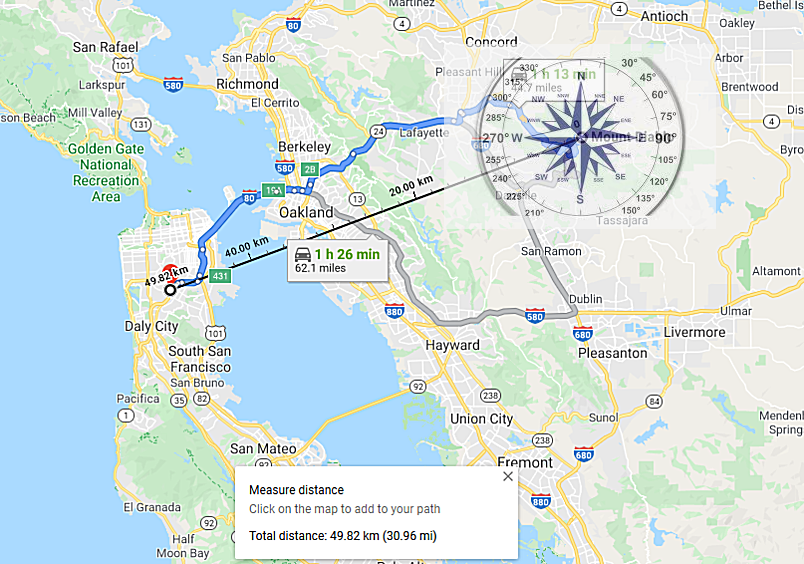
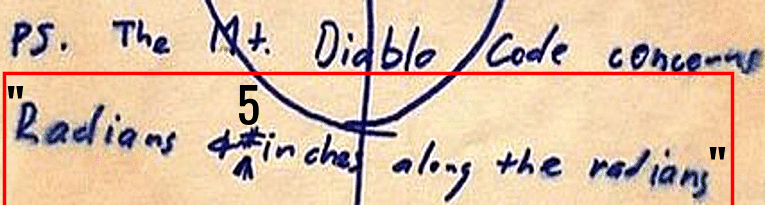
The center of the red circle is 246.2 degrees, showing the inaccuracy of the crude drawing by Zodiac The Zodiac Killer's measurements were probably nothing more than a rough guide in 1970, which is why he placed SFPD next to the crude circle to help us on our way. Therefore, it was quite surprising to discover that both Yuba Gap and the center of the punch-hole were situated extremely close to 5 radians and Magnetic North (at most a one degree error). The distance between the Sahara Tahoe Hotel & Casino and Yuba Gap, and the home of Donna Lass and Yuba Gap measured 6.83 and 6.86 inches respectively (an 83% to 86 % accuracy over one inch). Both distances were approaching 44 miles by crow. A distance of 44.8 miles would have been 7 inches.



























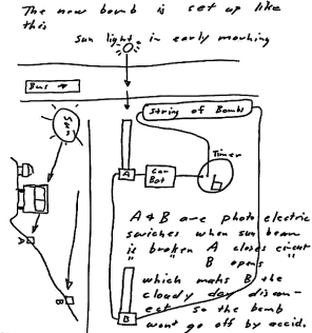
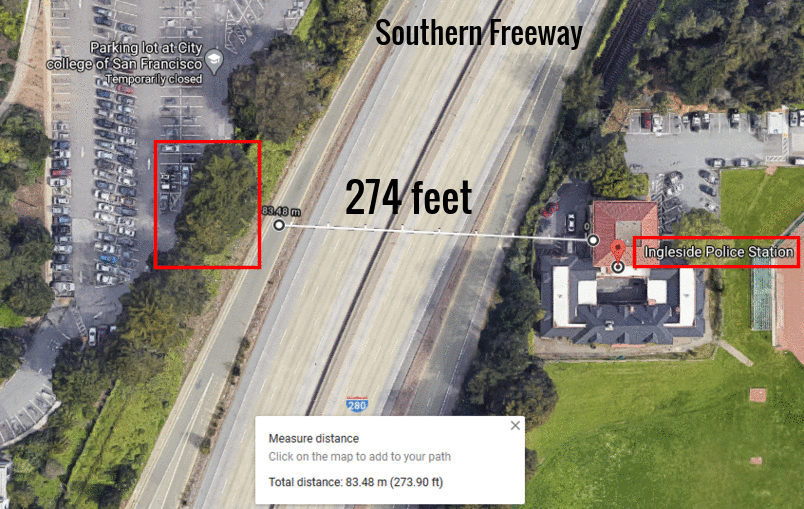
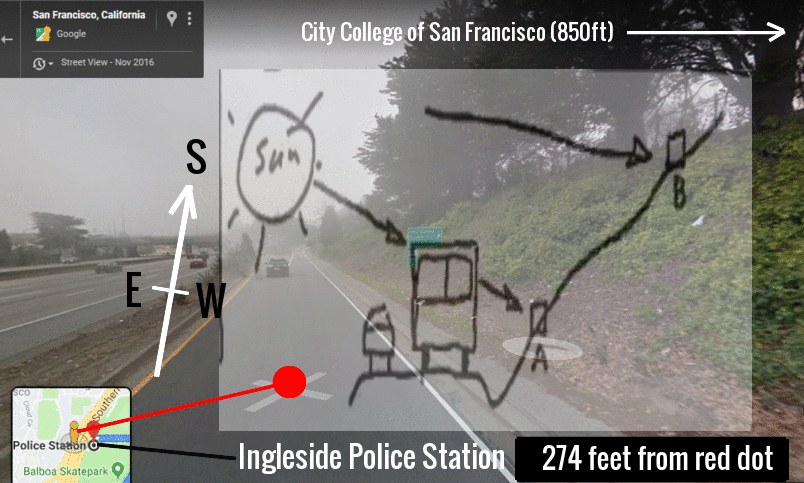



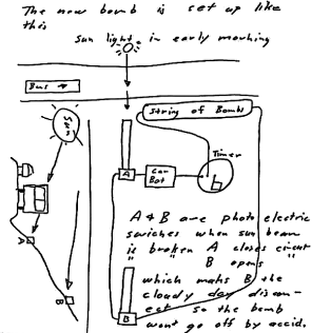

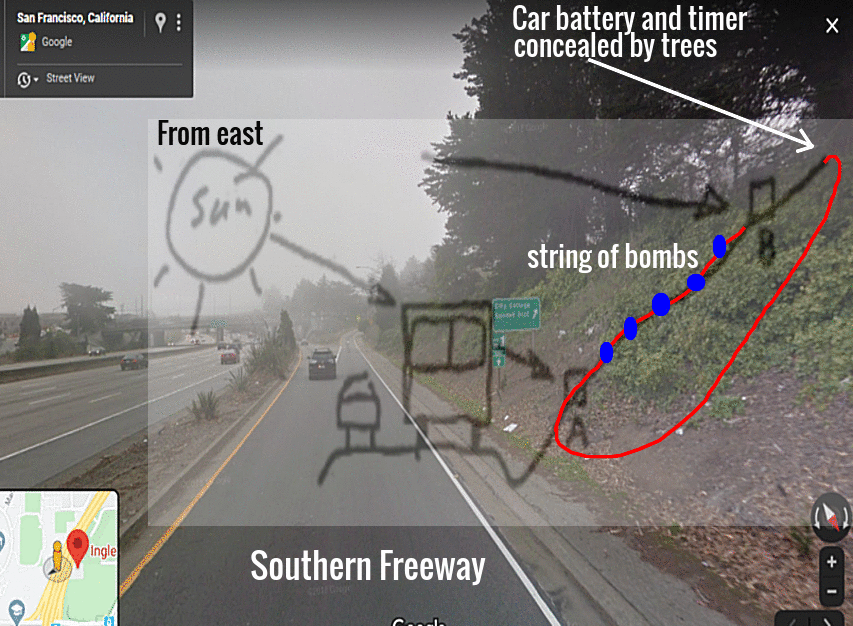

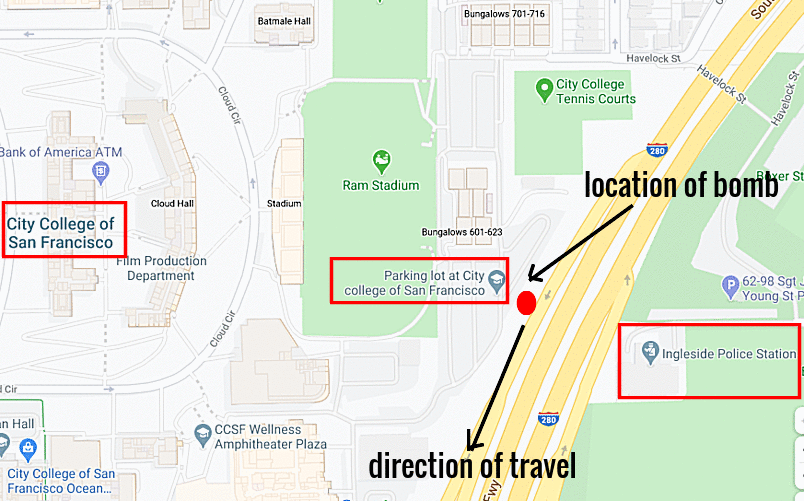





















 RSS Feed
RSS Feed